On the importance of NLP scaling
Estimated reading time: 2 minutesDuring my master’s thesis at KULeuven on optimal control, one of the take-aways were that it’s important to scale your variables. It helps convergence if the variables are in the order of 0.01 to 100.
Master student Thomas Durbin stumbled upon a dramatic example of bad scaling in practice. He works on optimal control for rockets. As a first toy problem, he studied a 1D rocket the must attain a certain height at $t=100\,\mathrm{s}$, with minimal expenditure of fuel. Following good engineering practice, he used SI base units to write the code.
The gist of the code is as follows (complete code here):
m0 = 500000; % start mass [kg]
yT = 100000; % final height [m]
g = 9.81; % gravity 9.81 [m/s^2]
alpha = 1/(300*g); % kg/(N*s);
opti = casadi.Opti();
% Decision variables [height;velocity;mass]
x = opti.variable(3,N+1);
y = x(1,:); % height
v = x(2,:); % velocity
m = x(3,:); % mass
u = opti.variable(1,N); % Control vector
% Dynamic constraints
rocket_ode = @(x,u) [x(2);u/x(3)-g;-alpha*u];
for k = 1:N
opti.subject_to(x(:,k+1) == x(:,k) + rocket_ode(x(:,k),u(:,k))*dt);
end
% Boundary conditions
opti.subject_to(x(:,1) == [0;0;m0]);
opti.subject_to(y(N+1) == yT);
The solution is quite interesting:

Optimal control of rocket problem.
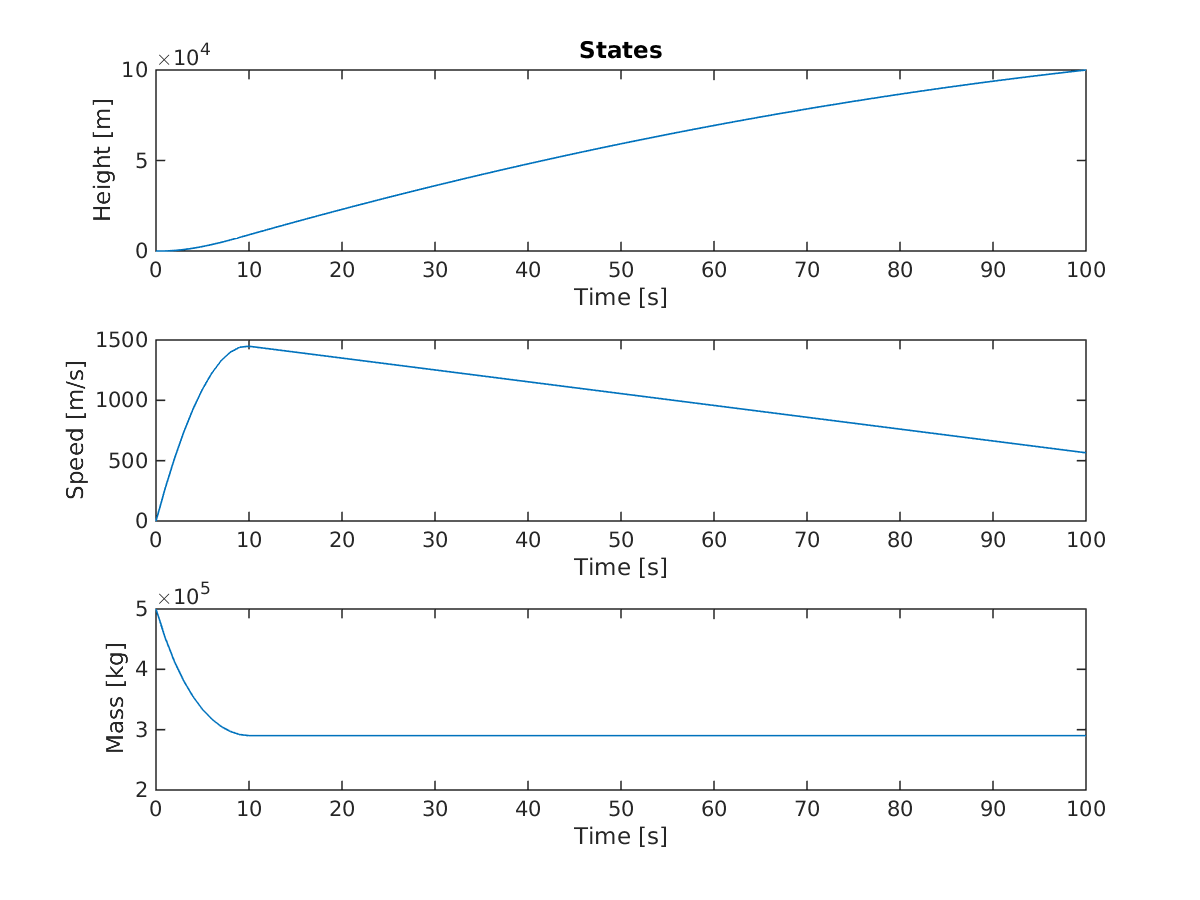
optimal states of rocket problem
But the focus is here on convergence. It’s pretty lousy.
semilogy(sol.stats.iterations.inf_du)
semilogy(sol.stats.iterations.inf_pr)
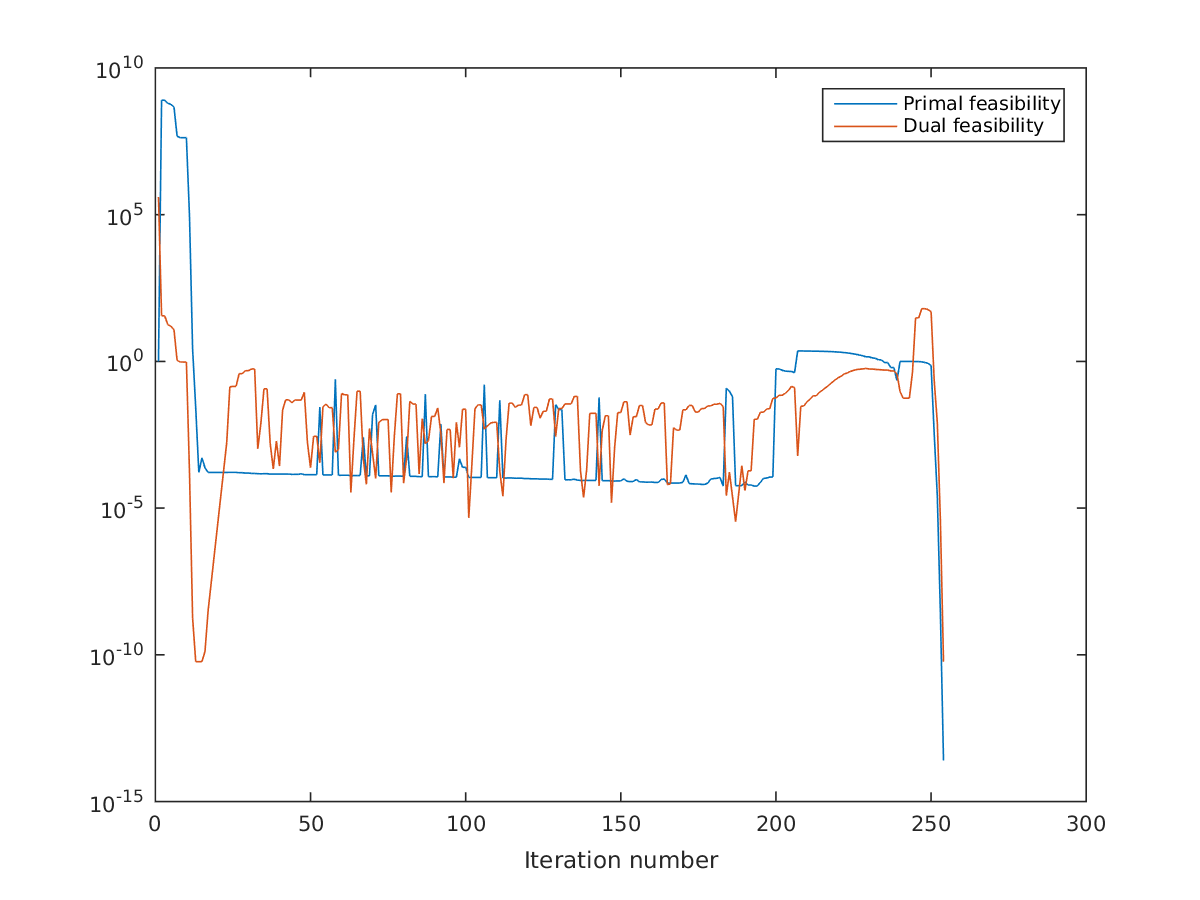
Convergence
x = repmat([1e5;2000;300e3],1,N+1).*opti.variable(3,N+1);
u = 1e8*opti.variable(1,N); % Control vector
Exact same solution, wildly different convergence:
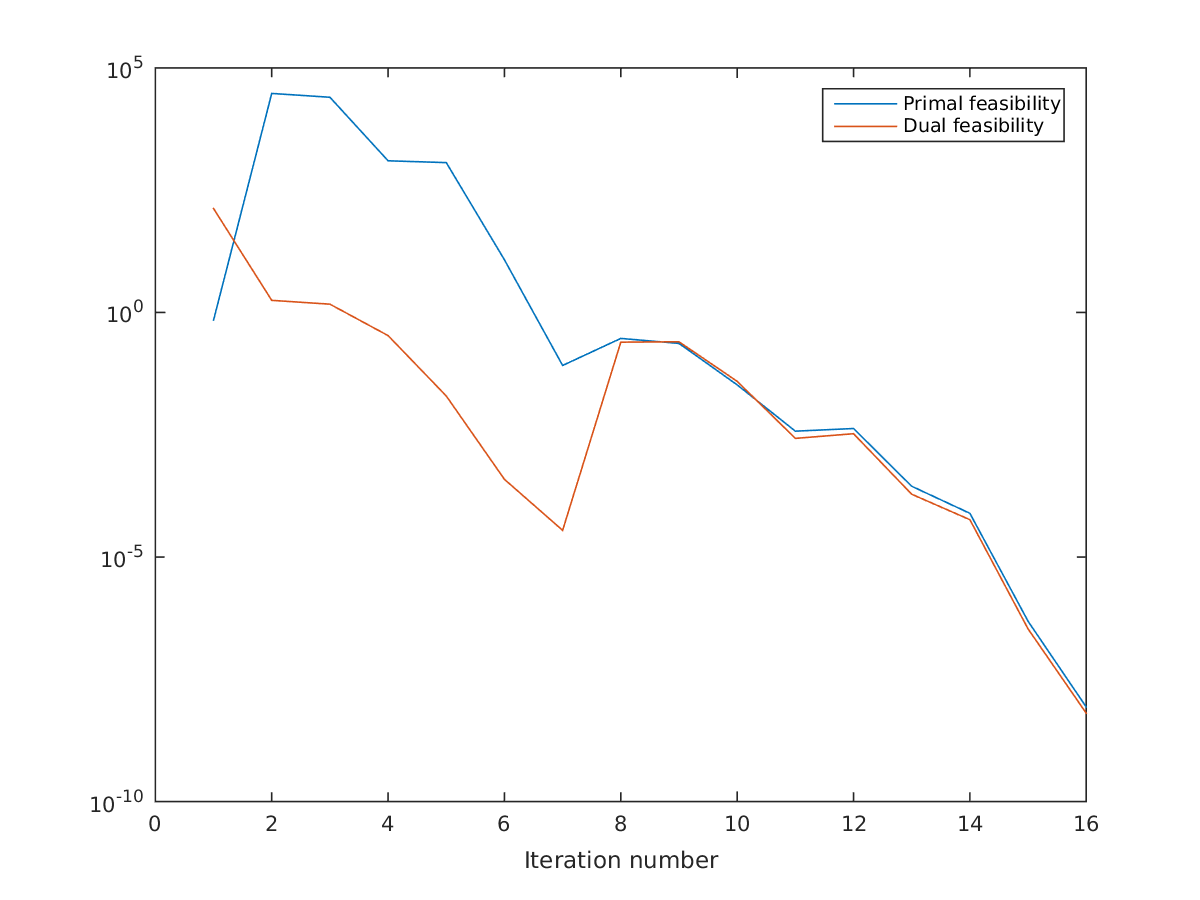
Convergence scaled
In conclusion, even if you are using an exact Hessian (which is default in CasADi), and even with a numerical backend (IPOPT) that provides auto-scaling, it’s still good practice to scale your NLP!
Addendum 2018-04-09
Guidelines for scaling involve more than just scaling of the variables. In IPOPT, objective and constraints (but not variables) are scaled automatically, using first-order sensitivities at the initial guess. This is vital for the above example to work. Without it, we need to scale objective and constraints ourselves:
for k = 1:N
opti.subject_to(x(:,k+1)./x_nom == (x(:,k) + rocket_ode(x(:,k),u(:,k))*dt)./x_nom);
end
...
opti.minimize((m(1)-m(N+1))/m_nom); % minimize fuel consumption
(complete code here)